Ветровые нагрузки

Для газоотводящих труб, представляющих собой высотные сооружения башенного типа, ветровая нагрузка имеет определяющее значение.

Сила и характер ветра, преимущественные направления сильных ветров определяется климатическими условиями и рельефом местности. Ветер редко бывает ровным, обычно наблюдаются порывы, вызванные торможением частиц воздуха о поверхность земли, конвекционными токами между различно нагретыми слоями, трением между слоями, движущимися с различной скоростью. Это приводит к пульсации скорости ветра. Интенсивность порывов ветра затухает с высотой. Порывы ветра характеризуются коэффициентом порывистости, являющимся отношением наибольшей скорости в порыве к средней за определенный промежуток времени. Коэффициент порывистости убывает с увеличением средней скорости ветра. Период пульсации ветра – от нескольких минут при большой величине средней скорости и до одной минуты при малой.

Статистическая обработка показала, что для высоты 20м можно принять коэффициент пульсации m = 0,25...0,35, для высот более 20м над поверхностью земли его определяют по формуле:

[,

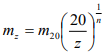где z - высота рассматриваемой точки, n = 8...12.

Сама природа ветра, когда на среднюю скорость накладываются порывы ветра, подсказывает представление ветровой нагрузки в виде двух компонент, одна из которых статическая, другая динамическая, тогда расчетный скоростной напор запишем в виде: q_р = n(q₀ + q_д), где n - коэффициент надежности по ветровой нагрузке, учитывающий возможное повышение нормативного скоростного напора q₀. Если ввести в формулу коэффициент пульсации скоростного напора m, определяемый ранее, и коэффициент динамичности, учитывающий реакцию сооружения на пульсацию ветра ξ, тогда расчетный скоростной напор ветра q_p = nq₀ (1 + ξm) , или q_p = nβq₀ , где β = 1 + ξm - коэффициент, учитывающий динамический характер воздействия порывов ветра. Действие порывов ветра на сооружении зависит от периода свободных колебаний и, что не менее важно, от затухания, характеризуемого чаще всего логарифмическим декрементом δ. Последний зависит от вида основного материала и конструктивного решения. Декремент затухания, определяемый опытным путем, принимают по данным о поведении подобных конструкций.

Рисунок 1. Коэффициент динамичности в зависимости от периода свободных колебаний сооружений

1. для гибких стальных сооружений (δ ≈ 0.1)
2. для металлических и деревянных сооружений (δ ≈ 0.15)
3. для железобетонных и каменных сооружений (δ ≈ 0.3)

Влияние порывов ветра на сооружение становится пренебрежимо малым, если период его собственных колебаний меньше 0,25сек. Период свободных колебаний сооружения находят обычным путем, после чего по графику, представленному на рисунке 1, находят коэффициент ξ для рассматриваемого вида конструкций, а затем – коэффициент β.

Коэффициент надежности по ветровой нагрузке n согласно СНиП равен 1,4, а вообще он зависит от назначения сооружения, планируемого срока службы и роли ветра в общем комплексе нагрузок, поэтому для дымовых труб он может приниматься до 1,5.

При проектировании уникальных сооружений большой высоты требуется более тщательное рассмотрение ветровой нагрузки, в котором наряду с рациональным назначением величины скоростного напора ветра большое внимание уделяют аэродинамическому комплексу вопросов.

Ветровую нагрузку на высокие сооружения консольного типа высотой менее 150 м допускается определять при учете свободных колебаний только по первой форме, т.е. по основному тону. Высокие сооружения консольного типа высотой более 150м рассчитывают на ветровую нагрузку с учетом не более первых трех форм колебаний.

Довольно часто наблюдаются перечные к потоку ветра колебания многих видов конструкций в виде цилиндра кругового очертания. Рассмотрим более подробно поведение круглого цилиндра в потоке воздуха.

Воздух обладает вязкостью, поэтому не может быть полного (плавного) обтекания. Слой, непосредственно прилегающий к цилиндру, не скользит свободно, а как бы прилипает к стенке, в результате чего возникают тангенциальные силы, направленные по касательной к поверхности тела. Эти силы и являются собственно силами трения. Силы вязкости вносят качественные изменения в картину обтекания.

Рисунок 2. Распределение давления по поверхности круглого цилиндра в потоке вязкой жидкости

Равнодействующая распределенных сил, действующих на стенки цилиндра, не равна нулю. Эту силу называют лобовым сопротивлением, составляющими которой являются силы трения и собственно давление.

Силы вязкости приводят к отрыву пограничного слоя и образованию позади тела вихреобразного движения жидкости (рис. 3). Давление вязкой жидкости на цилиндр в точке А почти не отличается от давления при обтекании его идеальной жидкостью. Но движение в пограничном слое тормозится и частицы жидкости приходят в точки Б и В с меньшими скоростями, чем в случае обтекания его идеальной жидкостью, т.е. он будут обладать меньшей кинетической энергией. В точках Д^/ и Д^// давление поэтому будет больше, чем в точках Б и В, но меньше p_А. В результате этого струи воздуха отрываются от цилиндра, так как не могут проникнуть в область Д^/ДД^//, заполненную вихреобразно движущейся жидкостью. Отрыв пограничного слоя вносит качественное изменение в обтекание тела потоком жидкости, которое не ограничивается лишь появлением лобового сопротивления, а сопровождается образованием вихрей, срывающихся с цилиндра и уносящихся потоком жидкости. Они рассеиваются далеко позади цилиндра. Явление вихреобразования происходит так: по любой нормали к поверхности цилиндра скорость жидкости постепенно возрастает от нулевой, которую имеет слой, непосредственно прилегающий к стенке, до скорости потока за пределами пограничного слоя, толщина которого мала. Объем жидкости в пограничном слое обладает моментом количества движения относительно оси, нормальной к плоскости потока и проходящей через центр объема. Такое движение жидкости обладает завихренностью, поэтому наряду с поступательным движением жидкости происходит и вращательное движение. Тонкие слои неустойчивы, они распадаются на отдельные вихри, уносимые потоком. Вихри располагаются за цилиндром в шахматном порядке, так как симметричное расположение вихрей – один над другим в дорожке – неустойчиво, что подтверждается многочисленными опытами и наблюдениями натуры.

Рисунок 4 Схема вихревой дорожки за круглым цилиндром

При отрыве вихря с цилиндра возникает подъемная сила, заставляющая его перемещаться в направлении поперек потока до тех пор, пока не установится равновесие. После этого цилиндр под влиянием восстанавливающей силы (упругости материала) начнет двигаться в противоположном направлении. Если скорость потока такова, что через промежуток времени, равный полупериоду колебаний, сорвется вихрь с другой стороны, то возникнет подъемная сила обратного знака, стимулирующая начавшиеся под влиянием восстанавливающей силы движение. Через полупериод снова возникнет из-за срыва вихря подъемная сила, которая будет поддерживать возникшие поперечные к потоку колебания.

Реакция сооружения может быть особенно сильной, когда происходит захватывание частоты образования вихрей собственной частотой сооружения (явление ветрового резонанса).

Частота срыва вихрей в большом интервале чисел Рейнольдса определяется числом Струхаля: Sh = nd / V , где d-диаметр цилиндра, м; n-частота свободных колебаний сооружения, Гц, V – скорость ветра, м/с. Для цилиндра, при всех числах Рейнольдса, кроме интервала очень малых чисел, Sh = 0,2. Отсюда критическая скорость ветра, при котором возникает явление ветрового резонанса, определяется формулой V_кр =5 nd.

При скорости ветра 25м/с и более амплитуды поперечных к ветру колебаний малы, а движения нерегулярны. Это позволяет не проводить дополнительного расчета на ветровой резонанс, если критическая скорость ветра выше 25м/с.

Результирующий динамический изгибающий момент M ^/ под воздействием ветровой нагрузки при «резонансной» скорости V_кр и аэродинамических сил, вызывающих моменты в плоскости, перпендикулярной потоку, рассчитывается по формуле геометрического сложения: M ^/ = √M²_д + M²_Vкк, где V_кр > 10м/c, но не более 25м/с.

Изгибающий момент M_Vкр определяется с учетом динамического коэффициента β.

При V_кр ≤ 10м/c расчетный изгибающий момент разрешается принимать равным M_д.

Действующие на сооружение аэродинамические силы определяются по формул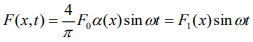е , где 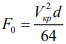- наибольшая амплитуда силы , кг/м, у свободного конца консольного цилиндра; 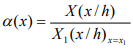- коэффициент формы колебаний;

X (x/h) - функция, определяющая первую форму свободных колебаний сооружения;

x - текущая координата, отсчитываемая по вертикали от начала координат;

x₁ - расстояние от сечения с наибольшей амплитудой до начала координат;

h - высота сооружения; t - время, сек; ω - круговая частота первой формы свободных колебаний сооружения.

Для упруго защемленного в фундаменте консольного цилиндрического сооружения имеем:

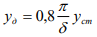, где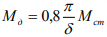

y_д, M_д - статический прогиб и изгибающий момент в рассматриваемом сечении под действием нагрузи F₁ (x);

δ - логарифмический декремент затухания;

0,8-коэффициент, учитывающий малую вероятность возникновения плоскопараллельного потока ветра по всей высоте сооружения.

Картина обтекания круглого цилиндра определяется в основном местом отрыва пограничного слоя, толщина которого мала. Это открывает путь управления колебаниями с помощью небольших по высоте препятствий – интерцепторов, так как не стоит сильно увеличивать ветровую нагрузку. Наилучшее действие оказывают спиральные интерцепторы, кроме того, они на меньшую величину повышают сопротивление конструкции ветру. Исследовались аэродинамические устройства в виде намотки проволоки по спирали вдоль цилиндра для создания сдвига фаз в срыве вихрей по высоте, тем самым достигалось уменьшение раскачивающей силы, вызванной срывом вихрей. Выяснено, что не всякая намотка проволоки вдоль цилиндра гасит колебания. Из всех рассмотренных вариантов проволочных гасителей наилучшим оказался вариант с намоткой четырех проволок с относительной толщиной d_п / D ≈ 1/200 под углом φ ≈ 11⁰ . Имеются и другие типы аэродинамических устройств.

Круглые цилиндры раскачиваются со значительно большей амплитудой, чем круглые усеченные конусы, что объясняется изменением частоты срыва вихрей по высоте последних. Поэтому при коничности дымовых труб более 0,012 расчет их на ветровой резонанс допускается не производить.

• Основы проектирования дымовых труб. Основные факторы и исходные данные для разработки проекта (Страница 1)
• Расчет высоты и выходного диаметра трубы. Расчет выходного диаметра и высоты трубы для обеспечения естественной тяги. Расчет высоты трубы при принудительной тяге (Страница 2)
• Основы аэродинамического расчета дымовых труб. Особенности внутренней аэродинамики (Страница 3)
• Диффузоры и их аэродинамика (Страница 4)
• Самоокутывание газоотводящих труб (Страница 5)
• Основы теплотехнического расчета (Страница 6)
• Основы силового расчета (Страница 7)
• Нагрузки и воздействия, реакция на них сооружения, особенности учета при расчете и проектировании. Нормативные и расчетные значения нагрузок (Страница 8)
• Особенности учета собственного веса. Температурные технологические воздействия (Страница 9)
• Ветровые нагрузки (Страница 10)
• Нормативные и расчетные значения прочностных и других характеристик материалов и грунтов. Проектирование ствола трубы (Страница 11)
• Проектирование и расчет оснований и фундаментов (Страница 12)

Подробную информацию про разработку проектной документации можно найти на странице о проектировании.